 En la Figura
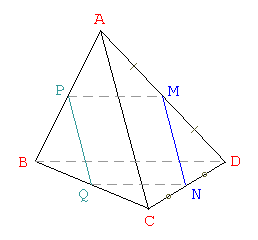
En la Figura::: M: Punto medio de AD
::: N: Punto medio de CD
::: M y N ∈ Plano Secante
::: Construímos dicho Plano Secante trazando PM y QN paralelas a BD
::: ☐PMNQ es la sección del Plano Secante pedido
::: En ΔABD, M es punto medio y PM // BD → PM = BD/2 = a/2
::: En ΔBCD, N es punto medio y QN // BD → QN = BD/2 = a/2
::: En ΔACD, M y N son puntos medios → MN = AC/2 = a/2
::: En ΔABC, P y Q resultan ser puntos medios → PQ = AC/2 = a/2
Finalmente
::: Perímetro de ☐PMNQ = PM + MN + QN + PQ = a/2 + a/2 + a/2 + a/2
::: ⇒ Perímetro de ☐PMNQ = 2a
VOLVER A LA PREGUNTA ::: UNI 2010-I: MATEMATICA

 ::: x3 - 7x2 + 15x - 9 = ( 1/logx(3/5) )
::: x3 - 7x2 + 15x - 9 = ( 1/logx(3/5) ) Ecuación
Ecuación ::: Nos dicen que la OEM se propaga en el vacío. Por tanto su velocidad de propagación será: C = 3×108 m/s
::: Nos dicen que la OEM se propaga en el vacío. Por tanto su velocidad de propagación será: C = 3×108 m/s En el ciclo de Carnot se cumple:
En el ciclo de Carnot se cumple: Fórmula
Fórmula Dato: Completa la primera vuelta en 1 s y ωo = 0
Dato: Completa la primera vuelta en 1 s y ωo = 0 El mínimo cambio de temperatura se produce cuando justo las piezas entran en contacto (como se muestra en la figura)
El mínimo cambio de temperatura se produce cuando justo las piezas entran en contacto (como se muestra en la figura) ::: Sea ∠BAC = α → ∠CDB = 4α ∧ ∠ACB = 5α
::: Sea ∠BAC = α → ∠CDB = 4α ∧ ∠ACB = 5α

 ::: Fig. 1: ƒ es sobreyectiva
::: Fig. 1: ƒ es sobreyectiva  Dato
Dato En la figura,
En la figura,  La ecuación de movimiento:
La ecuación de movimiento: Tenemos
Tenemos Tenemos
Tenemos En la figura
En la figura En la figura
En la figura
 Tenemos el siguiente gráfico:
Tenemos el siguiente gráfico: ::: S: Área de la región triangular
::: S: Área de la región triangular Donde:
Donde:

 Para la lente A se tiene:
Para la lente A se tiene:
