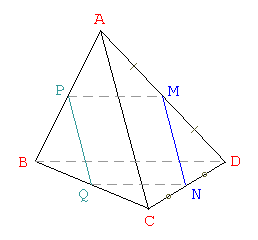
En la Figura::: M: Punto medio de AD
::: N: Punto medio de CD
::: M y N ∈ Plano Secante
::: Construímos dicho Plano Secante trazando PM y QN paralelas a BD
::: ☐PMNQ es la sección del Plano Secante pedido
::: En ΔABD, M es punto medio y PM // BD → PM = BD/2 = a/2
::: En ΔBCD, N es punto medio y QN // BD → QN = BD/2 = a/2
::: En ΔACD, M y N son puntos medios → MN = AC/2 = a/2
::: En ΔABC, P y Q resultan ser puntos medios → PQ = AC/2 = a/2
Finalmente
::: Perímetro de ☐PMNQ = PM + MN + QN + PQ = a/2 + a/2 + a/2 + a/2
::: ⇒ Perímetro de ☐PMNQ = 2a
VOLVER A LA PREGUNTA ::: UNI 2010-I: MATEMATICA
