Solucion 2.7

Observando la figura:

• Considerando solo la componente vertical del movimiento de un fragmento de mineral, tenemos:
     1,25 = gt²/2 → t = 0,504818 .... [1]
• Dicho tiempo t es también el válido para la componente horizontal del movimiento. Así:
     4 < vt < 6 ⇒ 7,92 < v < 11,885
VOLVER AL PROBLEMA

Solucion 2.6

Observemos la siguiente figura:

• El Sistema está en equilibrio. Luego:
    Fuerzas verticales: f = W => uN = mg .... [1]
    Fuerzas horizontales: N = F => N = kx .... [2]
• [2] en [1] => x = mg/uk => x = 1,962 cm
VOLVER AL PROBLEMA

Solucion 2.5

• Nombramos:
    M: Masa de la Tierra.
    M_L: Masa de la Luna.
    R: Radio de la Tierra.
    R_L: Radio de la Luna.
    g_L: Gravedad Lunar.
    G: Constante de Gravitación Universal.

• En la Tierra g = GM/R² ; En la Luna g_L = GM_L/R_L²
     => g_L = g·(M_L/M)(R_L/R)^-2
    Datos: M_L/M = 0,01255 y R_L/R = 0,273 => g_L = 1,65191

• Finalmente aplicamos Conservación de la Energía en los puntos A y B que se muestran en la figura:
     mg_Lh = mv²/2
     v² = 2g_Lh => v = 1,81764 m/s
VOLVER AL PROBLEMA

Solucion 2.4

En un gráfico F vs. x el área bajo la curva nos da el trabajo de la respectiva fuerza F.

• El área entre x = 0 y x = 15 la dividimos en A₁, A₂ y A₃.
• Sea W_F: Trabajo de la Fuerza F entre x = 0 y x = 15.
     => W_F = A₁ + A₂ + A₃
     => W_F = 402,5 J.
VOLVER AL PROBLEMA

Solucion 2.3

• Sabemos que I = ∆P , donde I : Impulso y P : Cant. de mov.
=> F∆t = ∆P ..... [1]
• Tenemos 32 partículas por segundo => ∆t = 1/32 s. por partícula.
• v_a = v_d = v (choque elástico)
• Aplicando conservación de Energía entre el punto más elevado y el más inferior: mgh = mv²/2 => v = sqrt(2gh)
• ∆P = 2mv => Finalmente de [1]:
=> F = 2mv/∆t = 64m*sqrt(2gh) donde h = 2,74 m; g: gravedad
=> F = 53,49455 N. (Que es la lectura que medirá la balanza)
VOLVER AL PROBLEMA

Solucion 2.2

En la figura se muestran diferentes pautas de un MAS, siendo
    k: constante elástica del resorte,
    x_m: amplitud de oscilación,
    v_m: velocidad máxima.

• Denominamos

    E_k: Energía Cinética.
    E_p: Energía Potencial del resorte.
    E_t: Energía Mecánica del Oscilador

    Sabemos: E_k + E_p = E_t, Luego E_k = E_t - (k/2)x² ..... [1]

• Tenemos la ecuación dato: E_k = 0,2 - 20x² ..... [2]

• De [1] y [2]:
    E_t = 0,2 J => I. V
    k = 40 N/m. Pero E_t = (k/2)x_m² => x_m = 0,1 m. => II. F

• Sea w la frecuencia angular de oscilación
    => w = sqrt(k/m) = sqrt(40/0,25) = 12,649 rad/s => III. V
VOLVER AL PROBLEMA

Solucion 2.1

• f = 4 Hz => T = 1/f = 0,25 s => I. V

• Del gráfico se observa que λ = 40 cm => II. F

• Sea v la velocidad de propagación: v = fλ = 160 cm/s = 1,6 m/s
=> III. V
VOLVER AL PROBLEMA

Solucion 2.0

• El sistema está en equilibrio => E = W ; E: fuerza de empuje, W: Peso del bloque
• => ρ_l*V_sumergido = ρ*V_bloque ; pero V_sumergido = 3V_bloque/4
• Finalmente: ρ_l = 4ρ/3
VOLVER AL PROBLEMA

Solucion 1.9

• Sea l_o la longitud inicial y l_f la longitud final
=> l_f = l_o + 2,5*10^-2*l_o
• Sea C_l el coeficiente térmico de dilatación lineal
=> ∆l = C_l*∆T*l_o
=> 2,5*10^-2*l_o = 2,5*10^-4*∆T*l_o => ∆T = 100 ºC
VOLVER AL PROBLEMA

Solucion 1.8

Se tiene 1 l. de H₂O a 20 ºC.

• La Potencia producida en el resistor: P = V²/R = 484 W.
• La capacidad calorífica del H₂O: C_v = 74,53 J/mol K
1 mol H₂O es Equivalente a 18,01528 x 10^-3 Kg ; 1 l. H₂O = 1 Kg. H₂O
• Q = C_v*∆T. Para que hierva el Agua se debe llegar a los 100 ºC
=>Q = 74,53 x (10³/18,01528) x 80 J = 330963,5 J
• Sea t el tiempo que se requiere para que el agua comienze a hervir
=> t = Q/P = 683,8 s. => t = 11 min. 23,8 s.
VOLVER AL PROBLEMA

Solucion 1.7

En la figura de arriba tenemos el caso para Q > 0. Abajo se muestra para Q < 0.

Observando la figura vemos: V = kQ/R , Donde V es el potencial en la superficie del globo de radio R y carga Q
Observese que Q es negativa => Conforme R crece (al inflar el globo) el Potencial V también crece (se hace menos negativo)
También conforme R se hace muy grande, el Potencial V se acerca a cero desde valores negativos. Finalmente:

VOLVER AL PROBLEMA

Solucion 1.6

• Sea P_v la potencia que se disipa en verano

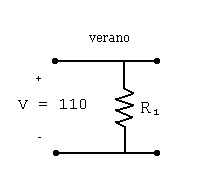=> P_v = V²/R₁ => R₁ = 110²/1100 => R₁ = 11

• Sea P_i la potencia que se disipa en invierno

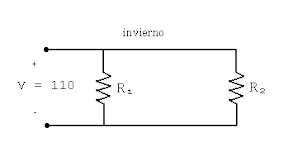=> P_i = V²/R₁ + V²/R₂ => 2200 = 1100 + 110²/R₂
=> R₂ = 11 => R₁ + R₂ = 22 Ω.
VOLVER AL PROBLEMA

Solucion 1.5

Observando la figura, en la ecuación [1] tenemos que para el caso en que la balanza marca cero en el Ecuador => N = 0
=> La nueva aceleración normal sería: a_N = g => T = 2π*sqrt(R/g)
=> T/T_o = 2π*sqrt(R/g)/T_o , Reemplazando los valores:
T/T_o = 0,05384
VOLVER AL PROBLEMA

Solucion 1.4

MN es aproximadamente paralelo a AB => ∆MNF ~ ∆ABF
=> MN/NF = AB/BF => MN/8 = 3/28
=> MN = 0,857 cm.
Del gráfico se deduce que la altura de la imagen es igual a MN.
VOLVER AL PROBLEMA

Solucion 1.3

Ecuación Básica: hf = hf_o + E_kmax ...... [1]; h: constante de Planck, f: frecuencia (= c/λ , λ: longitud de onda y c: velocidad de la luz)
Dado λ en nm: hf = hc/λ = (1242/λ) eV
• Para λ₁ = 780 nm y E_kmax1 = 0,37 eV. En [1]: hf_o = 1,22231 eV
• Para λ₂ = 410 nm. Otra vez en [1]: E_kmax2 = 1,806961 eV.
VOLVER AL PROBLEMA

Solucion 1.2

El campo magnético B: B(t=0)=2 ; B(t=sqrt(3))=0

=> B(t)=2-2t/sqrt(3)

Φ = B(t)*A*cos30 = sqrt(3) - t

ε = -dΦ/dt => ε = 1
VOLVER AL PROBLEMA

Solucion 1.1

O: Circuncentro ;  R: Circunradio ; r: Inradio 
OM, ON y OQ : Mediatrices ;  ON' = ha ; OQ' = hb ; OM' = hc
x = MR ; y = NS ; z = QT

• QUEREMOS HALLAR EL VALOR DE  x+y+z

• HALLEMOS x

    • <R'MO = <N'OC = <A ,  MO = OC = R
       => ∆R'MO = ∆N'OC -> MR' = ON' = ha
    • x = MR = MR'+R'R ;  R'R = OQ' = hb
       => x = ha+hb  ...... [1]

• HALLEMOS y

    • <S'NO = <Q'OA = <B ,  NO = OA = R
       => ∆S'NO = ∆Q'OA -> NS' = OQ' = hb
    • y = NS = NS'+S'S ;  S'S = OM' = hc
       => y = hb+hc  ...... [2]

• HALLEMOS z

    • <T'QO = <M'OB = <C ,  QO = OB = R
       => ∆T'QO = ∆M'OB -> QT' = OM' = hc
    • z = QT = QT'+T'T ;  T'T = ON' = ha
       => z = hc+ha  ...... [3]

• Sumando [1], [2] y [3]:

    • x+y+z = 2(ha+hb+hc)
    • Usando Propiedad 1.4 : x+y+z = 2(R+r) = 2(6+2)
    • => x+y+z = 16 m.

VOLVER AL PROBLEMA

Solucion 1.0

Nos piden: Area ∆TBO Trazamos FQ y GQ, luego BFQG es un paralelogramo. -> 9 (Area ∆FBO) = Area ∆ABC Trazamos QS // FG -> SFGQ es un paralelogramo. En ∆ABQ con cevianas BP y QS aplicamos Propiedad 1.1 -> 3 (Area ∆SBR) = 2 (Area ∆RBQ) -> 3 (Area ∆FBT) = 2 (Area ∆TBO) -> 15 (Area ∆TBO) = Area ∆ABC -> Area ∆TBO = 3 cm²
VOLVER AL PROBLEMA